Loi uniforme continue

En théorie des probabilités et en statistiques, les lois uniformes continues forment une famille de lois de probabilité à densité. Une telle loi est caractérisée par la propriété suivante : tous les intervalles de même longueur inclus dans le support de la loi ont la même probabilité. Cela se traduit par le fait que la densité de probabilité d'une loi uniforme continue est constante sur son support.

Elles constituent donc une généralisation de la notion d'équiprobabilité dans le cas continu pour des variables aléatoires à densité ; le cas discret étant couvert par les lois uniformes discrètes.

Une loi uniforme est paramétrée par la plus petite valeur ${\displaystyle a}$ et la plus grande valeur ${\displaystyle b}$ que la variable aléatoire correspondante peut prendre. La loi uniforme continue ainsi définie est souvent notée ${\displaystyle {\mathcal {U}}(a,b).}$

Les densités associées aux lois uniformes continues sont des généralisations de la fonction rectangle en raison de leurs formes.

Caractérisation

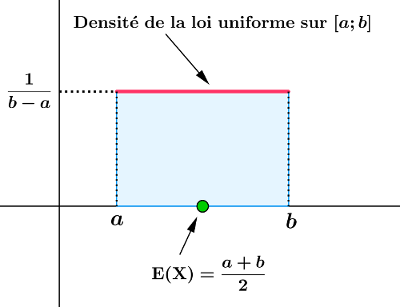
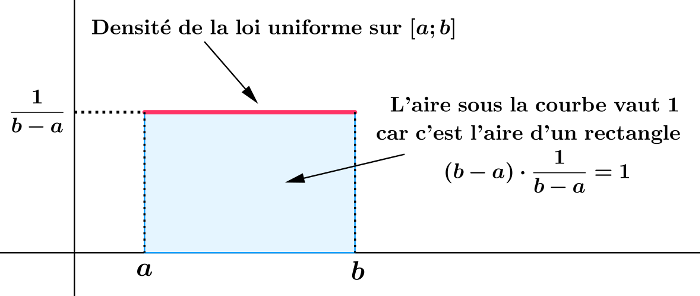
Densité

La densité de probabilité de la loi ${\displaystyle {\mathcal {U}}(a,b)}$ est une fonction porte sur l'intervalle [a, b] :

${\displaystyle \mathrm {f} (x)={\begin{cases}{\dfrac {1}{b-a}}&{\text{pour }}a\leq x\leq b,\\0&{\text{sinon}}.\end{cases}}}$

Fonction de répartition

La fonction de répartition de la loi ${\displaystyle {\mathcal {U}}(a,b)}$ est :

${\displaystyle \mathrm {F} (x)={\begin{cases}0&{\text{pour }}x$

Fonctions génératrices

Fonction génératrice des moments

La fonction génératrice des moments de la loi ${\displaystyle {\mathcal {U}}(a,b)}$ est :

${\displaystyle M_{X}=\mathbb {E} [{\rm {e}}^{tX}]={\frac {{\rm {e}}^{tb}-{\rm {e}}^{ta}}{t(b-a)}}.}$

Elle permet de calculer tous les moments non centrés, m_k :

${\displaystyle m_{1}={\frac {a b}{2}},}$

${\displaystyle m_{2}={\frac {a^{2} ab b^{2}}{3}},}$

${\displaystyle m_{k}={\frac {1}{k 1}}\sum _{i=0}^{k}a^{i}b^{k-i}.}$

Ainsi, pour une variable aléatoire suivant la loi ${\displaystyle {\mathcal {U}}(a,b),}$ l'espérance est m₁ = (a   b)/2, et la variance est m₂ − m₁² = (b − a)²/12.

Fonction génératrice des cumulants

Pour n ≥ 2, le n-ième cumulant de la loi uniforme continue sur l'intervalle [0, 1] est b_n/n, où b_n est le n-ième nombre de Bernoulli.

Propriétés

Statistiques d'ordre

Soit X₁, ..., X_n un échantillon i.i.d. issu de la loi ${\displaystyle {\mathcal {U}}(0,1).}$ Soit X_(k) la k-ième statistique d'ordre de l'échantillon. Alors la distribution de X_(k) est une loi bêta de paramètres k et n − k   1.

L'espérance est :

${\displaystyle \mathbb {E} [X_{(k)}]={k \over n 1}.}$

Ce fait est utile lorsqu'on construit une droite de Henry.

La variance est :

${\displaystyle \mathbb {V} [X_{(k)}]={k(n-k 1) \over (n 1)^{2}(n 2)}.}$

Aspect uniforme

La probabilité qu'une variable uniforme tombe dans un intervalle donné est indépendante de la position de cet intervalle, mais dépend seulement de sa longueur ${\displaystyle (\ell ),}$ à condition que cet intervalle soit inclus dans le support de la loi. Ainsi, si X suit la loi ${\displaystyle {\mathcal {U}}(a,b)}$ et si ${\displaystyle [x,x \ell ]}$ est un sous-intervalle de [a, b], avec ${\displaystyle \ell >0}$ fixé, alors :

${\displaystyle \mathbb {P} {\big (}X\in [x,x \ell ]{\big )}=\int _{x}^{x \ell }{\frac {\mathrm {d} y}{b-a}}={\frac {\ell }{b-a}},}$

qui est indépendant de x. Ce fait motive la dénomination de cette loi.

Loi uniforme standard

Le cas particulier a = 0 et b = 1 donne naissance à la loi uniforme standard, notée ${\displaystyle {\mathcal {U}}(0,1).}$ Il faut noter le fait suivant : si u₁ est distribué selon une loi uniforme standard, alors c'est aussi le cas pour u₂ = 1 – u₁.

Loi uniforme sur une partie borélienne

À toute partie A de ${\displaystyle \mathbb {R} ^{d},}$ borélienne, dont la mesure de Lebesgue λ(A) est finie et strictement positive, on associe une loi de probabilité, appelée loi uniforme sur A, de densité de probabilité ƒ définie, pour tout ${\displaystyle x\in \mathbb {R} ^{d},}$ par :

${\displaystyle \mathrm {f} (x)\ =\ {\frac {1}{\lambda (A)}}\ \chi _{A}(x),}$

où χ_A est la fonction indicatrice (ou caractéristique), notée aussi 𝟙_A, de l'ensemble A. La densité ${\displaystyle \mathrm {f} }$ est donc nulle à l'extérieur de A, mais égale à la constante ¹⁄_λ(A) sur A.

Cette page traite principalement du cas particulier où d = 1 et où A est un intervalle [a, b] de ${\displaystyle \mathbb {R} .}$

Transport et invariance

Il peut sembler surprenant que les variables ${\displaystyle \{V_{1} V_{2}\}}$ et ${\displaystyle \{V_{1} V_{2} V_{3}\},}$ par exemple, soient indépendantes, alors qu'elles dépendent toutes deux de manière cruciale des variables ${\displaystyle V_{1}}$ et ${\displaystyle V_{2}.}$ C'est une conséquence particulière de la propriété d'invariance de la loi uniforme : par exemple, étant la mesure de Haar de ${\displaystyle \mathbb {R} \backslash \mathbb {Z} ,}$ elle est idempotente pour la convolution.

Distributions associées

Le théorème suivant stipule que toutes les distributions sont liées à la loi uniforme :

Ainsi, pour obtenir des tirages (indépendants) selon la loi répartie par ${\displaystyle \mathrm {F} ,}$ il suffit d'appliquer l'inverse de ${\displaystyle \mathrm {F} }$ à des tirages (indépendants) uniformes sur ${\displaystyle [0,1].}$

Voici quelques exemples d’application de ce théorème ${\displaystyle {\big (}U\sim {\mathcal {U}}(0,1){\big )}:}$

• ${\displaystyle Y=-{\tfrac {\ln U}{\lambda }}}$ suit la loi exponentielle de paramètre ${\displaystyle \lambda \ ;}$
• Y = 1 – U^1/n suit la loi bêta de paramètres 1 et n. Ceci implique que la loi uniforme standard est un cas particulier de la loi bêta, de paramètres 1 et 1.

On trouvera un tableau plus complet ici. Par ailleurs, l'art d'engendrer des variables aléatoires de lois arbitraires, par exemple à l'aide de variables uniformes, est développé dans Non-Uniform Random Variate Generation, de Luc Devroye, édité chez Springer, disponible sur le web.

Inférence statistique

Estimation de l'un des paramètres lorsque l'autre est connu

Cette section décrit l'estimation de la borne supérieure ${\displaystyle (b)}$ de la distribution ${\displaystyle {\mathcal {U}}(a,b),}$ au vu d'un échantillon de ${\displaystyle n}$ individus, la borne inférieure ${\displaystyle (a)}$ étant connue.

Estimation du maximum

Estimateur sans biais de variance minimale

Pour une loi uniforme sur ${\displaystyle [0,b]}$ avec ${\displaystyle b}$ inconnu, l'estimateur sans biais de valeur minimale (en) pour le maximum est donné par :

${\displaystyle {\hat {b}}_{MV}={\frac {k 1}{k}}m=m {\frac {m}{k}},}$

où ${\displaystyle m}$ est le maximum de l'échantillon et ${\displaystyle k}$ la taille de l'échantillon, échantillonné sans remise (bien que cette précision n'a aucune incidence dans le cas uniforme).

On obtient cette valeur par un raisonnement similaire au cas discret. Ce problème peut être vu comme un cas simple d'estimation de l'espacement maximal (en). Il est connu sous le nom de Problème du char d'assaut allemand, par son application d'estimation maximale de la production des chars d'assaut allemands pendant la Seconde Guerre mondiale.

Estimateur par maximum de vraisemblance

L'estimateur par maximum de vraisemblance est :

${\displaystyle {\hat {b}}_{ML}=m,}$

où ${\displaystyle m}$ est la valeur maximum dans l'échantillon, qui est aussi la statistique d'ordre maximale de l'échantillon.

Estimateur par la méthode des moments

L'estimateur par la méthode des moments est :

${\displaystyle {\hat {b}}_{MM}=2{\bar {X}},}$

où ${\displaystyle {\bar {X}}}$ est la moyenne de l'échantillon.

Estimation du milieu

Le milieu ${\displaystyle {\tfrac {a b}{2}}}$ de l'intervalle de la loi uniforme ${\displaystyle {\mathcal {U}}(a,b)}$ est à la fois la moyenne et la médiane de cette loi. Bien que la moyenne et la médiane de l'échantillon sont des estimateurs sans biais du milieu, ils ne sont pas aussi efficaces que le milieu de gamme de l'échantillon, i.e. la moyenne arithmétique du maximum et du minimum de l'échantillon, qui est l'estimateur sans biais de variance minimale du milieu (et aussi l'estimateur par maximum de vraisemblance).

Intervalle de confiance

Pour le maximum

On considère X₁, X₂, ..., X_n un échantillon de ${\displaystyle {\mathcal {U}}_{[0,L]},}$ où L est la valeur maximum dans la population. Alors X_(n) = max( X₁, X₂, ..., X_n ) a la densité de Lebesgue-Borel ${\displaystyle \mathrm {f} ={\frac {\mathrm {d} \mathbb {P} _{X_{(n)}}}{\mathrm {d} \lambda }}:}$

${\displaystyle \mathrm {f} (t)=n{\frac {1}{L}}\left({\frac {t}{L}}\right)^{n-1}1\!\!1_{[0;L]}(t)=n{\frac {t^{n-1}}{L^{n}}}1\!\!1_{[0;L]}(t),}$

où ${\displaystyle 1\!\!1_{[0,L]}}$ est la fonction caractéristique (ou indicatrice) de ${\displaystyle [0,L].}$

L'intervalle de confiance est mathématiquement incorrect, car ${\displaystyle \mathbb {P} ([{\hat {\theta }},{\hat {\theta }} \varepsilon ]\ni \theta )\geq 1-\alpha }$ ne peut être résolu pour ${\displaystyle \varepsilon }$ sans information sur ${\displaystyle \theta .}$ On peut cependant résoudre

${\displaystyle \mathbb {P} ([{\hat {\theta }},{\hat {\theta }}(1 \varepsilon )]\ni \theta )\geq 1-\alpha }$ pour ${\displaystyle \varepsilon \geq (1-\alpha )^{-1/n}-1}$ pour tout ${\displaystyle \theta }$ inconnu mais valide ;

on peut alors choisir le plus petit ${\displaystyle \varepsilon }$ possible vérifiant la condition ci-dessus. On note que la longueur de l'intervalle ${\displaystyle [{\hat {\theta }},{\hat {\theta }}(1 \varepsilon )]}$ dépend de la variable aléatoire ${\displaystyle {\hat {\theta }}.}$

Estimation simultanée des deux paramètres

Cette section décrit l'estimation des deux bornes ${\displaystyle (a;b)}$ de la distribution uniforme continue ${\displaystyle {\mathcal {U}}(a,b),}$ au vu d'un échantillon de ${\displaystyle n}$ individus.

Soient ${\displaystyle {\hat {a}}}$ et ${\displaystyle {\hat {b}}}$ les estimateurs respectifs des bornes inférieure ${\displaystyle (a)}$ et supérieure ${\displaystyle (b)}$ de la distribution mère, construits sur la base de l'échantillon contenant les ${\displaystyle n}$ modalités de la variable aléatoire ${\displaystyle X}$ issues de la distribution ${\displaystyle {\mathcal {U}}(a,b).}$

La méthode du maximum de vraisemblance aboutit à la sélection des minimum et maximum empiriques :

${\displaystyle {\begin{cases}{\hat {a}}&=&\min \,(x_{i})_{i=1,n}\\{\hat {b}}&=&\max \,(x_{i})_{i=1,n}.\end{cases}}}$

Ce couple d'estimateurs est biaisé : la probabilité qu'un ${\displaystyle n}$-échantillon capture le minimum ${\displaystyle (a)}$ ou le maximum ${\displaystyle (b)}$ permis par la distribution mère étant quasi-nulle, la moyenne d'un grand nombre d'observations sur de tels ${\displaystyle n}$-échantillons ne converge pas vers les bornes de ladite distribution mère :

${\displaystyle {\begin{cases}\mathbb {E} ({\hat {a}})&\geq &a\\\mathbb {E} ({\hat {b}})&\leq &b.\end{cases}}}$

La démonstration est produite plus bas.

Loi de distribution régissant ces estimateurs biaisés

Les densités de probabilité sont notées en minuscules (par ex. ${\displaystyle \mathrm {f} }$), les fonctions de répartition sont notées en majuscules (par ex. ${\displaystyle \mathrm {F} }$).

Densité de probabilité associée au couple d'estimateurs biaisés

${\displaystyle d^{2}\mathbb {P} \,\left(x\leq {\hat {a}}\leq x dx\,;\,y\leq {\hat {b}}\leq y dy\right)=\underbrace {{\frac {n\,\left(n-1\right)}{\left(b-a\right)^{n}}}\,\left(y-x\right)^{n-2}} _{f_{{\hat {a}},{\hat {b}}}(x,y)}\,dx\,dy.}$

Lois marginales régissant les minimum et maximum empiriques

Concernant l'estimateur de la borne inférieure ${\displaystyle ({\hat {a}})\ :}$

${\displaystyle \forall x\in [a,b]\;{\begin{cases}d\mathbb {P} \,(x\leq {\hat {a}}\leq x dx)&=&f_{\hat {a}}(x)\,dx&=&{\frac {n}{b-a}}\,{\Bigl (}{\frac {b-x}{b-a}}{\Bigr )}^{n-1}\,dx\\\mathbb {P} \,({\hat {a}}\leq x)&=&F_{\hat {a}}(x)&=&1-{\Bigl (}{\frac {b-x}{b-a}}{\Bigr )}^{n}.\end{cases}}}$

Par une démonstration similaire, on obtient pour l'estimateur de la borne supérieure ${\displaystyle ({\hat {b}})}$ :

${\displaystyle \forall x\in [a,b]\;{\begin{cases}\mathrm {d} \mathbb {P} \,(x\leq {\hat {b}}\leq x dx)&=&f_{\hat {b}}(x)\,\mathrm {d} x&=&{\frac {n}{b-a}}\,\left({\frac {x-a}{b-a}}\right)^{n-1}\,\mathrm {d} x\\\mathbb {P} \,({\hat {b}}\leq x)&=&F_{\hat {b}}(x)&=&\left({\frac {x-a}{b-a}}\right)^{n}.\end{cases}}}$

Convergence de ces estimateurs

La définition de la convergence d'un estimateur est donnée dans le document référencé .

Concernant l'estimateur de la borne inférieure (${\displaystyle {\hat {a}}_{n}}$ sur un n-échantillon) : ${\displaystyle \mathbb {P} \,(|{\hat {a}}_{n}-a|>\varepsilon )=\mathbb {P} \,({\hat {a}}_{n}>a \varepsilon )}$ car aucune valeur inférieure à a ne peut être observée. Donc :

${\displaystyle \mathbb {P} \,(|{\hat {a}}_{n}-a|>\varepsilon )=\left({\frac {b-a-\varepsilon }{b-a}}\right)^{n}=\left(1-{\frac {\varepsilon }{b-a}}\right)^{n}{\xrightarrow[{n\rightarrow \infty }]{}}\,0.}$

Une démonstration similaire s'applique pour l'estimateur de la borne supérieure.

${\displaystyle ({\hat {a}};{\hat {b}})}$ forme donc un couple d'estimateurs convergents.

Biais de ces estimateurs

Lorsque l'on multiplie les échantillons (de taille ${\displaystyle n}$ donnée), la moyenne des observations ne tend pas vers le couple de bornes ${\displaystyle (a,b)}$ de la distribution mère :

${\displaystyle {\begin{cases}\mathbb {E} ({\hat {a}})&=&a {\frac {b-a}{n 1}}\\\mathbb {E} ({\hat {b}})&=&b-{\frac {b-a}{n 1}}.\end{cases}}}$

Ces deux estimateurs ne sont qu'asymptotiquement sans biais, i.e. lorsque la taille ${\displaystyle n}$ de l'échantillon tend vers l'infini.

Recherche d'estimateurs sans biais

Le couple d'estimateurs ${\displaystyle ({\hat {\hat {a}}}\,;\,{\hat {\hat {b}}})}$ défini ci-dessous est sans biais :

${\displaystyle {\begin{cases}{\hat {\hat {a}}}&=&{\hat {a}}-{\frac {{\hat {b}}-{\hat {a}}}{n-1}}&=&{\frac {n\,{\hat {a}}-{\hat {b}}}{n-1}}\\{\hat {\hat {b}}}&=&{\hat {b}} {\frac {{\hat {b}}-{\hat {a}}}{n-1}}&=&{\frac {n\,{\hat {b}}-{\hat {a}}}{n-1}}.\end{cases}}}$

Le calcul de ces estimateurs (avec ou sans biais) ne nécessite pas la connaissance des paramètres ${\displaystyle (a;b)}$ de la distribution mère.

Les lois de distribution qui régissent le couple d'estimateurs sans biais sont plus complexes à déterminer. Le document donne les lois suivantes :

Densité de probabilité associée au couple d'estimateurs sans biais

${\displaystyle d^{2}\mathbb {P} \,\left(x\leq {\hat {\hat {a}}}\leq x dx\,;\,y\leq {\hat {\hat {b}}}\leq y dy\right)=\underbrace {{\frac {n\,\left(n-1\right)^{n}}{\left(n 1\right)^{n-1}\,\left(b-a\right)^{n}}}\,\left(y-x\right)^{n-2}} _{f_{{\hat {\hat {a}}},{\hat {\hat {b}}}}(x,y)}\,dx\,dy.}$

Lois marginales régissant chacun des deux estimateurs sans biais

Sachant que la variable ${\displaystyle {\hat {\hat {a}}}}$ admet comme support l'intervalle ${\displaystyle \left[{\frac {n\,a-b}{n-1}}\,;\,b\right]}$ :

${\displaystyle {\begin{cases}\forall x\leq a&d\mathbb {P} \,\left(x\leq {\hat {\hat {a}}}\leq x dx\right)&=&{\frac {\left(n-1\right)^{n-1}}{n^{n-2}\,\left(b-a\right)^{n}}}\,\left[\left(b-x\right)^{n-1}-n^{n-1}\left(a-x\right)^{n-1}\right]\,dx\\\forall x\geq a&d\mathbb {P} \,\left(x\leq {\hat {\hat {a}}}\leq x dx\right)&=&{\frac {\left(n-1\right)^{n-1}}{n^{n-2}\,\left(b-a\right)^{n}}}\,\left(b-x\right)^{n-1}\,dx.\end{cases}}}$

Sachant que la variable ${\displaystyle {\hat {\hat {b}}}}$ admet comme support l'intervalle ${\displaystyle \left[a\,;\,{\frac {n\,b-a}{n-1}}\right]}$ :

${\displaystyle {\begin{cases}\forall y\leq b&d\mathbb {P} \,\left(y\leq {\hat {\hat {b}}}\leq y dy\right)&=&{\frac {\left(n-1\right)^{n-1}}{n^{n-2}\,\left(b-a\right)^{n}}}\,\left(y-a\right)^{n-1}\,dy\\\forall y\geq b&d\mathbb {P} \,\left(y\leq {\hat {\hat {b}}}\leq y dy\right)&=&{\frac {\left(n-1\right)^{n-1}}{n^{n-2}\,\left(b-a\right)^{n}}}\,\left[\left(y-a\right)^{n-1}-n^{n-1}\left(y-b\right)^{n-1}\right]\,dy.\end{cases}}}$

Intervalle de pari

On considère ici :

• une loi mère uniforme ${\displaystyle {\mathcal {U}}(a,b)}$ donnée et connue,
• le couple d'estimateurs avec biais formé par le minimum ${\displaystyle ({\hat {a}})}$ et le maximum ${\displaystyle ({\hat {b}})}$ empiriques déterminés sur un ${\displaystyle n}$-échantillon.

Les estimateurs considérés sont ceux avec biais car :

• leurs lois de distribution sont simples à manipuler ;
• le document référencé montre que construire des intervalles de pari à partir des estimateurs sans biais n'aboutit pas in fine à des intervalles plus réduits pour un niveau de confiance donné, et en explique la raison.

On cherche à connaître comment se répartissent les n-échantillons possibles formés à partir de la distribution mère ${\displaystyle {\mathcal {U}}\,(a,b)}$, en plaçant dans le plan ${\displaystyle \mathbb {R} ^{2}}$ :

• sur l'axe des abscisses, la borne inférieure ${\displaystyle (a)}$ de la distribution mère et les minima empiriques des échantillons ;
• sur l'axe des ordonnées, la borne supérieure ${\displaystyle (b)}$ de la distribution mère et les maxima empiriques des échantillons.

On note :

${\displaystyle {\begin{cases}m&=&{\text{valeur de}}\,{\hat {a}}&=&\min \,(x_{i})_{i=1,n}\\M&=&{\text{valeur de}}\,{\hat {b}}&=&\max \,(x_{i})_{i=1,n}.\end{cases}}}$

La distribution mère ${\displaystyle {\mathcal {U}}(a,b)}$ et la construction des estimateurs imposent la hiérarchie suivante : ${\displaystyle a\leq m\leq M\leq b.}$ Les échantillons issus de cette loi mère sont tous situés à l'intérieur du triangle rectangle formé par la droite ${\displaystyle x=a}$, la droite ${\displaystyle y=b}$ et la première bissectrice (cf. figure ci-contre).

Un bon échantillon (i.e. un échantillon représentatif de sa population mère) se caractérise par :

• un minimum empirique ${\displaystyle (m)}$ proche de ${\displaystyle a}$
• et un maximum empirique ${\displaystyle (M)}$ proche de ${\displaystyle b.}$

Le risque de pari ${\displaystyle (\alpha )}$ associé à un échantillon ${\displaystyle ({\hat {a}}=m\,;{\hat {b}}=M)}$ est défini par la probabilité de trouver un échantillon plus mauvais que lui, i.e. présentant :

• un minimum empirique supérieur ou égal à ${\displaystyle m,}$
• ou un maximum empirique inférieur ou égal à ${\displaystyle M.}$

Intervalle de pari sur le minimum empirique

L'expérimentateur choisit son risque de pari ${\displaystyle (\alpha )}$. Le risque de pari sur le minimum empirique est défini par l'équation suivante :

${\displaystyle \alpha =\mathbb {P} \,\left({\hat {a}}\geq m\;\forall {\hat {b}}\in \left[{\hat {a}}\,;\,b\right]\right)=\left({\frac {b-m}{b-a}}\right)^{n}\Rightarrow \,m_{1-\alpha }=b-(b-a)\cdot \alpha ^{\frac {1}{n}}}$

La surface de pari sur le minimum empirique au niveau de confiance ${\displaystyle (1-\alpha )}$ rassemble les échantillons qui vérifient : ${\displaystyle {\hat {a}}\in [a\,;m_{1-\alpha }]}$ et ${\displaystyle {\hat {b}}\in [{\hat {a}}\,;b]}$.

Intervalle de pari sur le maximum empirique

De façon similaire, le risque de pari sur le maximum empirique est défini par l'équation suivante :

${\displaystyle \alpha =\mathbb {P} \,\left({\hat {b}}\leq M\;\forall {\hat {a}}\in \left[a\,;{\hat {b}}\right]\right)=\left({\frac {M-a}{b-a}}\right)^{n}\Rightarrow \,M_{1-\alpha }=a (b-a)\cdot \alpha ^{\frac {1}{n}}}$

La surface de pari sur le maximum empirique au niveau de confiance ${\displaystyle (1-\alpha )}$ rassemble les échantillons qui vérifient : ${\displaystyle {\hat {b}}\in [M_{1-\alpha }\,;b]}$ et ${\displaystyle {\hat {a}}\in [a\,;{\hat {b}}]}$.

Surface de pari sur les deux bornes

La surface de pari est celle qui capture la proportion ${\displaystyle (1-\alpha )}$ des échantillons formés à partir d'une population mère ${\displaystyle {\mathcal {U}}\,(a,b)}$ donnée et connue.

Le problème dépend de la forme que l'on aura choisi de donner à cette surface, qui peut être un carré, un triangle, un quart de cercle, ... On choisit ici un triangle rectangle, de sommet ${\displaystyle P_{1}\,\left(a\,;\,b\right)}$ et dont l'hypoténuse est parallèle à la première bissectrice (cf. figure ci-contre). La raison est que la densité de probabilité associée au couple ${\displaystyle \left({\hat {a}}\,;\,{\hat {b}}\right)}$est constante le long d'un lieu ${\displaystyle y-x=Cte}$. Ceci permet de découper l'espace suivant une ligne iso-densité, minimisant ainsi la surface de pari pour capturer un effectif donné.

Les variables réduites classiques pour les distributions uniformes sont introduites afin de simplifier les calculs qui suivent :

${\displaystyle {\begin{cases}\varphi &=&{\frac {m-a}{b-a}}\\\psi &=&{\frac {M-a}{b-a}}\end{cases}}}$

Les relations de conversion du domaine réel en domaine réduit sont données par le tableau ci-dessous :

Exprimée dans le plan des coordonnées réduites, la surface pari au niveau de confiance ${\displaystyle (1-\alpha )}$ est constituée par l'intérieur du triangle rectangle de sommets :

${\displaystyle P_{1}{\begin{pmatrix}0\\1\end{pmatrix}}\;\;P_{2}{\begin{pmatrix}\delta \\1\end{pmatrix}}\;\;P_{3}{\begin{pmatrix}0\\1-\delta \end{pmatrix}}}$

La marge réduite ${\displaystyle \left(\delta \right)}$ est reliée au risque de pari ${\displaystyle \left(\alpha \right)}$ par l'équation suivante :

${\displaystyle \left(1-\delta \right)^{n-1}\,\left[1 \left(n-1\right)\delta \right]=\alpha }$

L'équation liant la marge réduite ${\displaystyle \left(\delta _{1-\alpha }\right)}$ au risque de pari ${\displaystyle \left(\alpha \right)}$ peut être résolue par la méthode du point fixe : la suite ${\displaystyle \left(x_{n}\right)}$ définie ci-dessous converge rapidement vers la solution, même avec une initialisation forfaitaire :

${\displaystyle {\begin{cases}x_{0}&=&{\frac {1}{2}}\\x_{n 1}&=&1-\left({\frac {\alpha }{1 \left(n-1\right)\,x_{n}}}\right)^{\frac {1}{n-1}}\end{cases}}}$

Le lieu des solutions est tracé ci-contre, en fonction de l'effectif de l'échantillon et du risque de pari ${\displaystyle \alpha }$.

Replacée dans le plan des coordonnées correspondant au problème réel de l'expérimentateur, la surface pari au niveau de confiance ${\displaystyle (1-\alpha )}$ est constituée par l'intérieur du triangle rectangle de sommets :

${\displaystyle P_{1}{\begin{pmatrix}a\\b\end{pmatrix}}\;\;P_{2}{\begin{pmatrix}a \delta _{1-\alpha }\,\left(b-a\right)\\b\end{pmatrix}}\;\;P_{3}{\begin{pmatrix}a\\b-\delta _{1-\alpha }\,\left(b-a\right)\end{pmatrix}}}$

Surface de confiance

Le point de vue est inversé par rapport à la section précédente :

• le n-échantillon est connu, et le couple des minimum et maximum empiriques obtenus est ${\displaystyle \left(m\,;M\right)}$ ;
• on veut connaître quelles populations mères ${\displaystyle {\mathcal {U}}\,(a,b)}$ auraient pu générer cet échantillon, au niveau de confiance ${\displaystyle (1-\alpha )}$ choisi par l'expérimentateur.

Il s'agit donc de recenser les populations mères qui contiennent l'échantillon en question dans leurs surfaces de pari respectives au niveau de confiance ${\displaystyle (1-\alpha )}$.

L'intégrale calculée lors de la démonstration qui établit la surface de pari en coordonnées réduites ${\displaystyle \left(\varphi \,;\,\psi \right)}$ reste inchangée, quelles que soient les raisons qui font varier ces coordonnées réduites :

• les variations du couple ${\displaystyle \left(m\,;M\right)}$ à population mère ${\displaystyle {\mathcal {U}}\,(a,b)}$ fixée,
• ou bien les variations des bornes ${\displaystyle \left(a\,;\,b\right)}$ de la population mère à échantillon ${\displaystyle \left(m\,;M\right)}$ fixé

La surface de confiance est obtenue par déréduction de la surface établie en coordonnées ${\displaystyle \left(\varphi \,;\,\psi \right)}$ pour le niveau de confiance ${\displaystyle (1-\alpha )}$, en cherchant ${\displaystyle \left(a\,;\,b\right)}$ à échantillon ${\displaystyle \left(m\,;M\right)}$ fixé. Cette surface de confiance est constituée par l'intérieur du triangle rectangle de sommets :

${\displaystyle Q_{1}{\begin{pmatrix}m\\M\end{pmatrix}}\;\;Q_{2}{\begin{pmatrix}{\frac {m-\delta _{1-\alpha }\,M}{1-\delta _{1-\alpha }}}\\M\end{pmatrix}}\;\;Q_{3}{\begin{pmatrix}m\\{\frac {M-\delta _{1-\alpha }\,m}{1-\delta _{1-\alpha }}}\end{pmatrix}}}$

Applications

En statistiques, lorsqu'une valeur p (p-value) est utilisée dans une procédure de test statistique pour une hypothèse nulle simple, et que la distribution du test est continue, alors la valeur p est uniformément distribuée selon la loi uniforme sur [0, 1] si l'hypothèse nulle est vérifiée.

Obtenir des réalisations de la loi uniforme

La plupart des langages de programmation fournissent un générateur de pseudo-nombres aléatoires, dont la distribution est effectivement la loi uniforme standard.

Si u est U(0, 1), alors v = a (b − a)u suit la loi U(a, b).

Obtenir des réalisations d'une loi continue quelconque

D'après le théorème cité plus haut, la loi uniforme permet en théorie d'obtenir des tirages de toute loi continue à densité. Il suffit pour cela d'inverser la Fonction de répartition de cette loi, et de l'appliquer à des tirages de la loi uniforme standard. Malheureusement, dans bien des cas pratiques, on ne dispose pas d'une expression analytique pour la fonction de répartition; on peut alors utiliser une inversion numérique (coûteuse en calculs) ou des méthodes concurrentes, comme la Méthode de rejet.

Le plus important exemple d'échec de la méthode de la transformée inverse est la Loi normale. Toutefois, la Méthode de Box-Muller fournit une méthode pratique pour transformer un échantillon uniforme en un échantillon normal, et ce de manière exacte.

Permutations aléatoires uniformes et loi uniforme

Des mathématiciens comme Luc Devroye ou Richard P. Stanley ont popularisé l'utilisation de la loi uniforme sur [0, 1] pour l'étude des permutations aléatoires (tailles des cycles, nombres eulériens, analyse d'algorithmes de tri comme le tri rapide, par exemple).

Construction d'une permutation aléatoire uniforme à l'aide d'un échantillon de loi uniforme

Soit ${\displaystyle U=(U_{1},U_{2},\dots ,U_{n})}$ une suite de variables aléatoires i.i.d. uniformes sur [0, 1], définies sur un espace probabilisé ${\displaystyle (\Omega ,{\mathcal {A}},\mathbb {P} )}$ (par exemple, définies sur ${\displaystyle \Omega =[0,1]^{n}}$ muni de sa tribu des boréliens et de sa mesure de Lebesgue, par ${\displaystyle U_{k}(\omega _{1},\omega _{2},\dots ,\omega _{n})\ =\ \omega _{k},}$ ou, de manière équivalente, par ${\displaystyle U(\omega )=\omega }$). Pour tout entier k compris entre 1 et n, posons

${\displaystyle \sigma (k,\omega )\ =\ \mathrm {Card} \left\{i\ \mathrm {tels~que} \ 1\leq i\leq n,\ \mathrm {et~tels~que} \ U_{i}(\omega )\leq U_{k}(\omega )\right\}.}$

Ainsi, ${\displaystyle \sigma (k,\omega )}$ s'interprète comme le rang de ${\displaystyle U_{k}(\omega )}$ dans l'échantillon, une fois celui-ci rangé dans l'ordre croissant.

La proposition ci-dessus reste vérifiée si la distribution de probabilité commune aux variables ${\displaystyle U_{i}}$ possède une densité, quelle qu'elle soit, et non pas seulement pour la densité uniforme. On peut même se contenter de variables i.i.d. dont la loi est diffuse (sans atomes) modulo une modification mineure de la démonstration. Cependant la loi uniforme est particulièrement commode pour diverses applications.

Nombres de descentes d'une permutation aléatoire, et nombres eulériens

Soit ${\displaystyle X_{n}(\omega )}$ le nombre de descentes d'une permutation ${\displaystyle \sigma (\omega )}$ tirée au hasard uniformément dans ${\displaystyle {\mathfrak {S}}_{n}.}$ Bien sûr,

${\displaystyle {\begin{aligned}\mathbb {P} \left(X_{n}=k\right)&={\frac {\mathrm {nombre~de~cas~favorables} }{\mathrm {nombre~de~cas~possibles} }}\\&={\frac {A(n,k)}{n!}},\end{aligned}}}$

où A(n,k) désigne le nombre de permutations de ${\displaystyle {\mathfrak {S}}_{n}}$ possédant exactement k descentes. A(n,k) est appelé nombre eulérien. Posons

${\displaystyle S_{n}=U_{1} U_{2} \dots U_{n}.}$

On a alors

Il en découle immédiatement un théorème central limite pour ${\displaystyle X_{n},}$ via le théorème de Slutsky.

Notes et références

Articles connexes

• Méthode de Box-Muller
• Droite de Henry
• Générateur de nombres pseudo-aléatoires
• Loi uniforme discrète
• Loi bêta

• Portail des probabilités et de la statistique