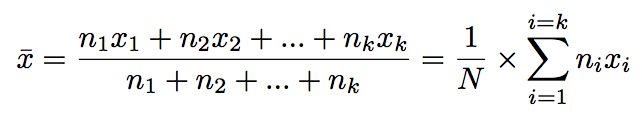Moyenne harmonique pondérée

En statistiques, si on considère le jeu de données suivant :

X = { x₁, x₂, ..., x_n}

et les poids associés :

W = { w₁, w₂, ..., w_n}

la moyenne harmonique pondérée se calcule de la manière suivante :

${\displaystyle {\bar {x}}=\sum _{i=1}^{n}w_{i}{\bigg /}\sum _{i=1}^{n}{\frac {w_{i}}{x_{i}}}}$

Si tous les poids sont égaux, la moyenne harmonique pondérée est la moyenne harmonique.

Il existe également des versions pondérées des autres moyennes. La plus connue est sans doute la moyenne arithmétique pondérée, appelée simplement moyenne pondérée. Un autre exemple de moyenne pondérée est la moyenne géométrique pondérée.

Voir aussi

• Moyenne arithmétique
• Moyenne géométrique
• Moyenne quadratique

• Portail des probabilités et de la statistique